Leonhard Euler was a Swiss astronomer, physicist engineer, and mathematician. Lauded for being one of the greatest mathematicians in history, Euler throughout his lifetime worked and introduced several important concepts mostly related to mathematics. He is also known for his work in fluid dynamics, mechanics, astronomy, optics and music theory, etc.
According to many historians, Euler is an irreplaceable figure whose contribution to the field of mathematics still remains the most prolific. With that being said, let’s revisit history and study Euler’s most significant contributions that keep his legacy alive even after centuries.
Early Life
Born in 1707, to Paul III Euler, a pastor of the Reformed Church, and Marguerite, who was a daughter of another pastor, Euler was the oldest of the four siblings. He had two younger sisters and one younger brother. Although Leonhard was born in Basel, Switzerland but soon after his birth, his father moved from Basel to Riehen, Switzerland, where he became a pastor and Euler spent most of his childhood.
At the time, Paul was friends with the Bernoulli family, who shared an interest and passion for mathematics. As a result, Paul took classes from one of the most prolific mathematicians of the time Jacob Bernoulli and Johann Bernoulli. This friendship and bond based on love for mathematics would have a huge influence on young Leonhard.
In Basel, Leonhard’s formal education was started while he lived with his maternal grandmother. In 1720, at just 13 years of age, Leonhard enrolled in the University of Basel. Soon, he received a Master of Philosophy based on a dissertation that was compared with the philosophies of Newton and Descartes. At the time, Leonhard received Saturday afternoon classes from Johann Bernoulli, who discovered that his student had an incredible for mathematics.
Initially, Leonhard’s father wanted him to become a pastor. However, encouraged by the results of Johann Bernoulli’s classes, he requested his father to let him become a mathematician. As a result, in 1726, Euler came out with a dissertation on the propagation of sound titled “De Sono”. His dissertation was unsuccessful in securing him a position at the University of Basel.
In 1727, Euler took part in the Prize Problem competition organized by the Paris Academy. The problem was to find the best way to replace the ship masts. Pierre Bouguer, who was termed as the “the father of naval architecture” won the competition and Euler came second. But after that, Euler won the annual prize twelve times.
Career
Saint Petersburg
While Leonhard was busy with his life, Johann Bernoulli’s two sons, Nicolaus and Daniel were working at the Imperial Russian Academy of Sciences located in Saint Petersburg. Unfortunately, in 1726, Nicolaus passed away after spending just a year in Russia due to appendicitis. As a result, Daniel took charge of his brother’s position and recommended that his vacated seat of physiology should be filled by his friend Euler.
In 1726, Euler accepted the offer but voluntarily delayed traveling to Saint Petersburg while waiting for his application status as a physics professor at the University of Basel, which was unsuccessful. In 1727, Euler arrived in Saint Petersburg. At the time, he was employed as a junior in the medical department but was then promoted to a senior position in the department of mathematics. Euler yet again came close to Daniel Bernoulli and mastered Russian. As a secondary job, he joined the Russian Navy as a mechanic.
At Saint Petersburg, Peter the Great had established an academy for improving education in Russia and closing the scientific gap with Western Europe. As a result, it was no surprise that it would attract foreign scholars like Euler. Additionally, the academy was financially stable and had a huge collection of books collected and managed by Peter himself. However, the academy offered very limited seats to keep the teaching burden in check.
The academy encouraged and promoted research while allowing its faculty to spend as much time pursuing scientific questions as possible. Even before Euler could arrive, Catherine I, the academy’s benefactress passed away. While she was alive, she ensured that the progressive policies laid down by her late husband continued. The nobility at the time grew suspicious of the academy’s foreign scientists and cut the funding, creating difficulties for Euler and his colleagues.
Following the death of Peter II, Euler gradually moved through the ranks of the academy and was made the professor of Physics in 1731 while turning down a promotion as a lieutenant in the Russian Navy. Two years later, Daniel Bernoulli had enough of the hostility and censorship by Saint Petersburg and left for Basel. Euler then took charge as the head of the mathematics department.
Berlin
After spending a sufficient amount of time in Russia, Euler also got concerned about the turmoil in Russia, and therefore, he left St. Petersburg in 1741 to take up a position offered by Frederick the Great of Prussia at the Berlin Academy. Euler spent 25 years in Berlin and wrote 380 articles. In Berlin, he wrote two articles, the introduction in analysin infinitorum and the institutions calculi differentialis, which would become his most renowned works.
In 1755, he was elected as the formal member of the Royal Swedish Academy of Sciences and the French Academy of Sciences. In addition to that, Euler was also asked to tutor Friederike Charlotte of Brandenburg-Schwedt, Frederick’s niece and the Princess of Anhalt-Dessau.
As a result, Euler wrote more than 200 letters to her during the early 1760s, which were later compiled. The complication of these letters was turned into a volume entitled Letters of Euler on different subjects in Natural Philosophy Addressed to a German Princess.
The work contained Euler’s contribution to physics and mathematics along with valuable insights into the personal life of Euler and religious beliefs. The book became the most popular amongst his publications, volumes, articles, and other works. It was translated into multiple languages while being published across the United States and Europe.
Considering that Euler shared a significant contribution to the Academy and was also considered as its candidate by Jean le Rond d’Alembert but Frederick II named himself the president. According to him, Euler was not a good debater and knew little beyond numbers and figures. He was right. Euler was known to argue on topics and subjects he knew little about. This put him in a rift with Voltaire who enjoyed a high position at Frederick’s court.
Contributions to Mathematics and Physics
Mathematical notation
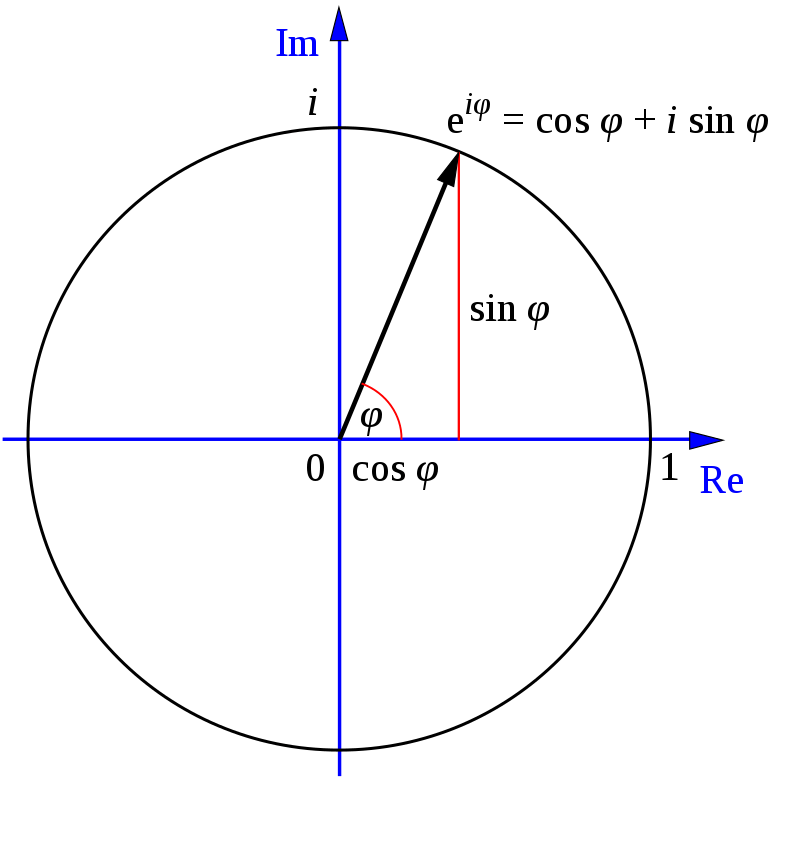
Euler came up with widely circulated textbooks that introduced and popularized several notational conventions. The most notable amongst which was the concept of function. Euler was the first individual to write f(x) to donate the function f applied to an argument x. Furthermore, he also introduced the trigonometric functions of modern notations such as the letter e of the natural logarithm’s base.
Additionally, he also introduced the Greek Letter Σ for summations and the letter I, to donate the imaginary unit.
Analysis
During the 18th century, the infinitesimal calculus was at the forefront of mathematical research, and the Bernoullis family was credited for much of the field’s early progress. Thanks to them, Euler’s interest grew in Calculus and soon he was following it as well. Even though most of Euler’s ideas are not acceptable according to the modern standards of mathematical rigor but his ideas led to significant advances.
It was Euler who introduced the use of logarithms and the exponential function in analytic proofs. He was able to successfully use power series to express several various logarithmic functions and even defined logarithms for both complex and negative numbers. As a result, the scope, as well as the application of logarithms, widely increased.
Euler’s formula eiπ + 1 = 0, was termed as the most remarkable formula in mathematics by Richard P. Feynman. Furthermore, Euler introduced a new method to solve quartic equations and gamma function to elaborate the higher transcendental functions theory. He determined a way to calculate integrals with complex limits.
Considering Euler’s introduction of analytic methods, it was clear that he pioneered different ways to solve theory problems. As a result, he joined two separate branches of mathematics and introduced analytic number theory, a new field of study. Moreover, he later came up with theories such as q-series, hypergeometric series, and hyperbolic trigonometric functions, etc.
Graph Theory
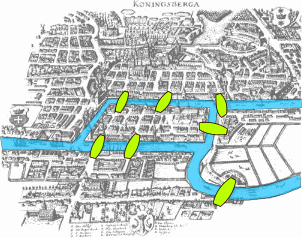
In 1735, Euler worked on a popular problem known as the Seven Bridges of Konigsberg and proposed a solution. The problem involved the city of Konigsberg, Prussia located on the Pregel River. It featured two large Islands that were connected to each other and the mainland using seven bridges. The question was whether there is a way that allows passing each bridge once and returning to the starting point.
According to Euler, it was not possible since there was no Eulerian Circuit. The Eulerian Circuit concept was introduced by Euler himself, which stated that it is basically a cycle or trail that starts and ends at the same vertex.
Physics, Astronomy, and Engineering
Most of Euler’s fame and success came from the fact that he was able to offer solutions to real-world problems analytically. In addition to that, he was also able to describe various applications of the Bernoulli numbers, Euler Numbers, and Fourier series, etc. along with e and π constants.
Euler also helped develop the Euler-Bernoulli beam equation, which served as the cornerstone of engineering. Not only did Euler use these analytical tools to solve classical mechanics but also celestial problems. During his career, he received several Prizes for his achievements in Astronomy. For instance, he was able to calculate the exact and accurate orbits of cornets and other celestial bodies, understanding the nature of cornets, and even calculating the sun’s parallax.
These studies helped and contributed to the accurate development of the longitude tables. Furthermore, Euler also made significant development in optics. At the time, when Newton’s corpuscular theory of light was in the spotlight, Euler rejected it. His papers dating the 1740s concluded that Euler’s work on optics sided more with Christiaan Huygens’s mode of thought on the wave theory of light.
Personal Life
Euler throughout his mathematical career experienced worsening eyesight. In 1738, he became almost blind in his right eye after nearly expiring from fever. Although Euler blamed the painstaking work on Cartography as the cause but the real reason behind his blindness remains disputed and speculated.
As his eyesight worsened during his stay in Germany, Frederick referred to him as “Cyclops”. Euler on the other hand stated that now he would have fewer distractions. Then, his left eye developed a cataract which was discovered in 1766. A failed surgical procedure as a result nearly left him totally blind. However, that did not stop him from working on new concepts and equations. His eyesight might have weakened but he compensated for it by using his exceptional memory and mental calculation skills. Despite having eye problems, Euler’s productivity at the end of the day increased and he could remember and re-call every line and page from his volumes and editions.
Return to Russia and Death
In 1760, Russia was engaged in a Seven Years’ War. As a result, Euler’s farm also experienced significant damage and was sacked by the advancing Russian troops. Upon learning about the event, General Ivan Petrovich Saltykov paid for the damages caused to the state. Additionally, the Empress Elizabeth of Russia later also offered 4000 roubles, which was a huge amount at the time.
Russia’s situation slightly improved upon Catherine the Great’s succession to the throne. Therefore, he accepted the invitation to return to St. Petersburg Academy. His conditions included 3000 rubles as annual salary, pension for his wife, and high-ranking positions for his sons. All conditions were accepted.
Euler was joined by his student Anders Johan Lexell and spent the rest of his remaining years in Russia. However, an unfortunate tragedy struck in 1771, which cost him his home and almost his life. In 1773, he lost his wife Katherine. After Katherine’s passing, Euler married her half-sister, Salome Abigail Gsell. The marriage ran until his last breath and Euler was elected as a Foreign Honorary Member of the American Academy of Arts and Sciences.
In 1783, Euler was at a lunch with his family, discussing Uranus, which was a newly discovered planet at the time when he collapsed and passed away due to brain hemorrhage.
Final Word
Euler’s work and contribution to the field of mathematics, physics, and astronomy, etc. earned him enough respect and popularity to be featured on the Swiss 10-franc banknote on several German, Swiss, and Russian postage stamps.
Although many mathematicians since then have introduced new concepts and equations but Euler’s remains the most famous as he laid the basis for major concepts we study today. Therefore, when it comes to discussing some of the biggest contributions to the field of mathematics, the Euler-ism phenomenon should not be ignored.